各种研究领域(包括无线定位方向)都会碰到参数估计的问题,这时常常会看到克拉美罗界 (Cramér–Rao bound) 这个东西。很多随机信号的书都会介绍什么是克拉美罗界,但初学者学起来往往很吃力,本文从直观上简单讨论一下克拉美罗界的各个方面。
什么是参数估计问题
假设一种最简单的情况:
一个物理量为,我们使用某种方式去观测它,观测值为
,由于存在噪声,此时
,
为高斯噪声,
。
这种情况下,我们自然会直接使用观测值去估计
,这时就会存在估计的误差,直观地理解,噪声的方差
越大,估计就可能越不准确。
为什么要讨论克拉美罗界
讨论克拉美罗界就是为了使用这个标准来衡量无偏估计量的性能。
采用上面的方式,使用去估计
,这个估计值会在真实值附近波动(看作随机变量)。我们需要使用一些标准来衡量这种估计的好坏,一个标准是估计值的平均,这里的这个估计量是无偏估计量。另一标准是这个估计值波动的剧烈程度,也就是方差。上面这个问题中,克拉美罗界就等于这个方差。
可是为什么不直接讨论方差而要去计算克拉美罗界呢,因为方差是针对某一种特定的估计量(或者理解为估计方式)而言的,在上面的例子中,方差是估计量的方差(
)。对于稍微复杂一点点的问题,对
的可以有各种不同的估计量,它们分别的方差是不同的。显然,对于无偏估计量而言,方差越小的估计方式性能越好,但是这个方差有一个下界,就是我们的克拉美罗界。
直观地理解克拉美罗界
克拉美罗界本身不关心具体的估计方式,只是去反映:利用已有信息所能估计参数的最好效果。
还是上面那个参数估计问题,当我们观察到的时候,我们可以知道真实值
的概率密度分布是以
为均值,
为方差的正态分布,即:
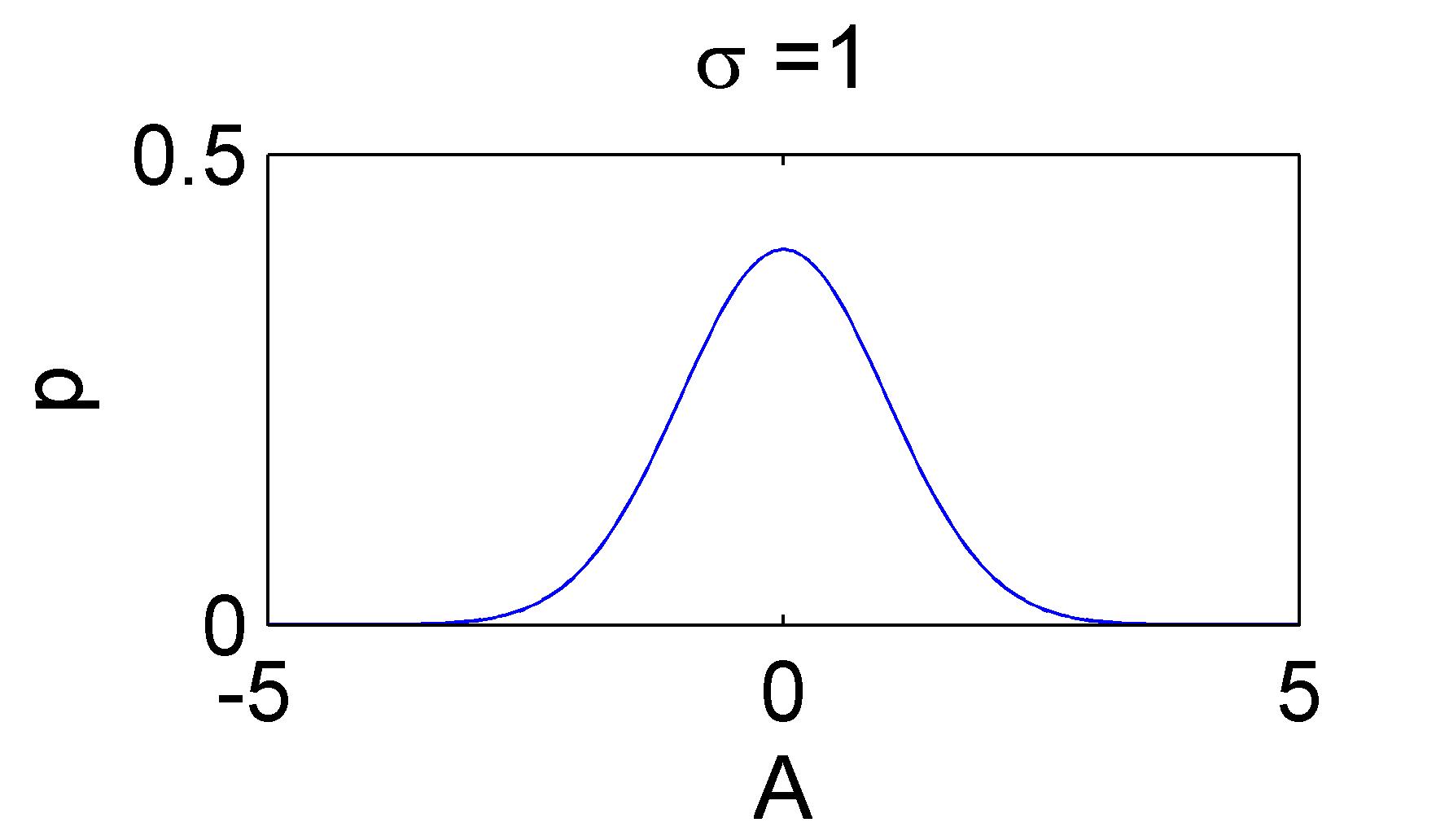
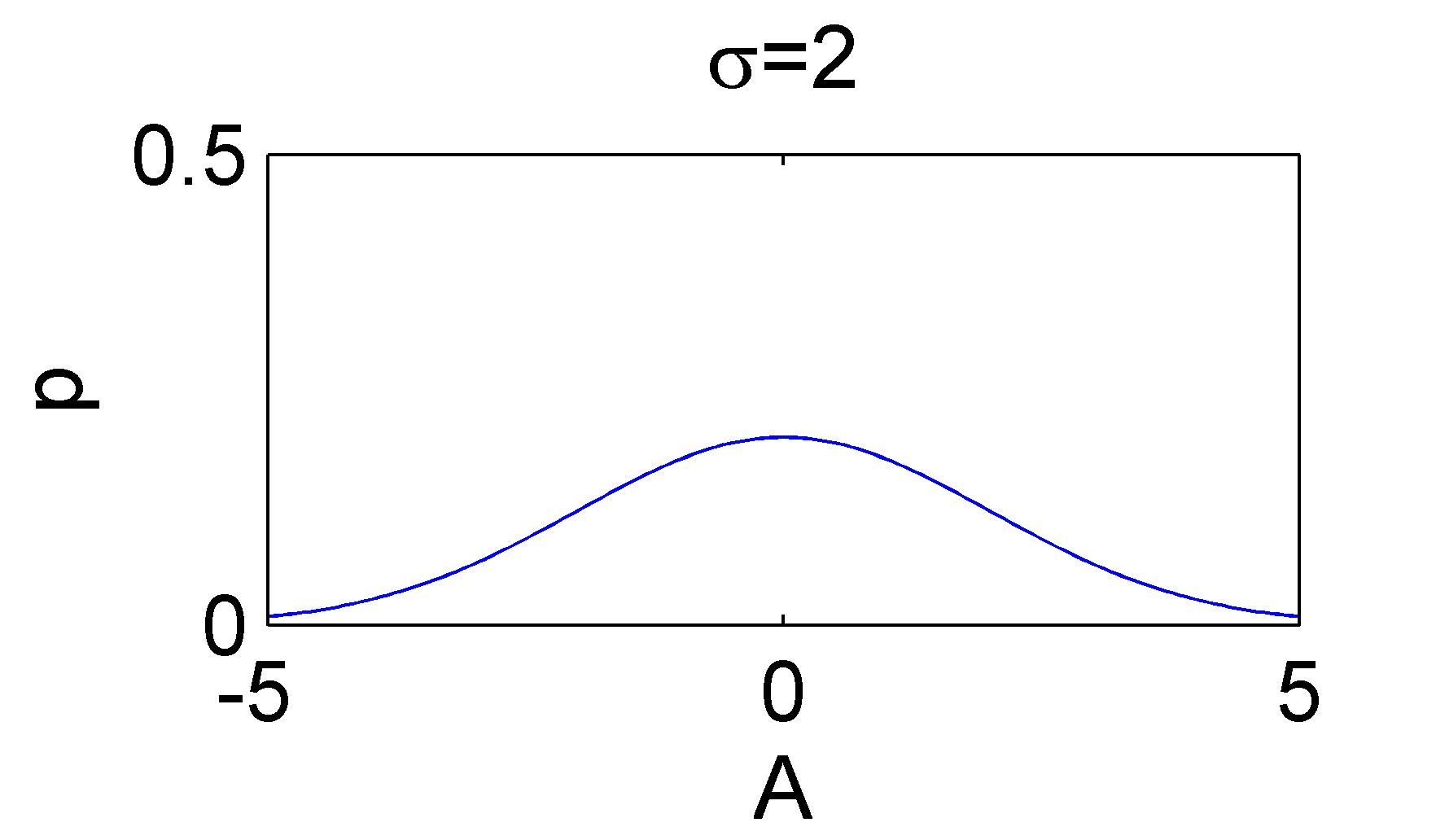
上图给出了两个似然函数的例子,直观地看,似然函数的“尖锐”性决定了我们估计位置参数的精度。这个“尖锐”性可以用对数似然函数峰值处的负的二阶导数来度量,即对数似然函数的曲率(对数似然函数就是在似然函数的基础山加一个自然对数,这样有利于计算)。计算过程我就不写了,有兴趣的可以自己算算,算完之后结果为:
,这里正好是噪声的方差的倒数,也就是噪声越小,对数似然函数越尖锐。
所以,可以这样理解,似然函数的“尖锐”程度的倒数(即对数似然函数的二阶导的倒数),就是克拉美罗界。
不同的估计量(估计方式)是什么意思
让我们来分析一个稍微复杂一点点的参数估计问题:
一个物理量为,我们使用某种方式去观测它,观测值为
和
,这是两个不同时刻的观测结果,一样的高斯噪声
。
这种情况下,我们要估计,正常人可能会采用估计量
,即前后两个观测的平均,也有人可能觉得这样计算量有点大,于是总是直接使用
去估计
,也有人觉得第二个观测值可能会受到系统影响而不准确,他更相信前面的观察值,于是总采取这样的估计量
。这三个估计量都是无偏的:
估计量的方差为:
估计量的方差为:
估计量的方差为:
比较上面的三种估计量,第一种的方差最小,它的估计效果较好。实际上,如果第二个观测值真的不太准确,也就是后一个高斯噪声较大,这样的话也许第二个估计量就比较合适了。
因此,不同的考虑方式可以产生各种不同的估计算法,这些不同的估计量都是在真实值附近波动的随机变量(有的有偏,有的无偏),它们分别的方差也是不一样的,但是数学家们证明了:任何无偏估计量的方差必定大于等于克拉美罗界。
克拉美罗界的基本计算
我们假设这两次观察互相独立,仅受相同的高斯白噪声影响,那么根据已有的信息,真实值的似然函数为两个正态的概率密度分布相乘:(注意:pdf实际上应该再进行归一化处理,但是我们之后使用对数似然函数,乘不乘归一化系数都无所谓,对数之后变成了常数,求导的时候就没了)
与之前一样,可以计算出对数似然函数的二阶导数,得到结果为:。实际上,当观测数目为
的时候,这个值将会是
。也就是说,使用多个观测值的信息时,对数似然函数越“尖锐”。这个二阶导数(曲率)更一般的度量是(下面用
来表示要估计的参数
):
它度量了对数似然函数的平均曲率(很多情况下曲率与的值有关,取数学期望使得它仅为
的函数),被称为数据
的Fisher信息
,直观地理解,信息越多,下限越低,它具有信息测度的基本性质(非负的、独立观测的可加性)。一般来说,Fisher信息的倒数就是克拉美罗界了,任何无偏估计量
的方差满足:
大多情况下,这个不等式的右边(克拉美罗界)是的函数。
克拉美罗界的标准定义
(定理:Cramer-Rao下限----标量参数)
假定PDF 满足“正则”条件(对于所有的
):
其中数学期望是对 求取的。那么,任何无偏估计量
的方差必定满足:
其中导数是在的真值处计算的,数学期望是对
求取的。而且,对于某个函数
和
,当且仅当
时,对所有达到下限的无偏估计量就可以求得。这个估计量是
,它是MVU估计量(最小方差无偏估计),最小方差是
。
总结
估计一个参数,根据已有信息得到了似然函数(或者pdf),这个pdf的“尖锐”程度的倒数(即对数似然函数的二阶导的倒数)就是克拉美罗界。克拉美罗界的计算不依赖具体的估计方式,它可以用来作为一个衡量估计方式好坏的标准,即估计量的方差越靠近克拉美罗界,效果越好。
(注:本文主要参考《统计信号处理基础-估计与检测理论》-国外电子与通信教材系列)
作者:
出处: 关于作者:目前主要研究领域为机器学习与无线定位技术,欢迎讨论与指正!版权声明:本文版权归作者和博客园共有,转载请注明出处。